Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
Вот схема типичного транзистора:
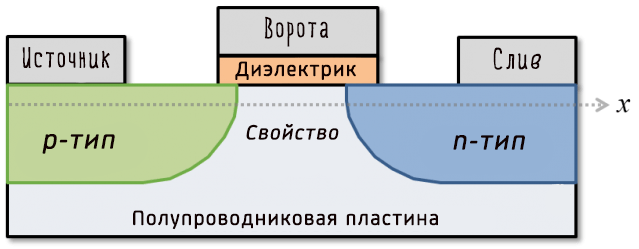
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.
Таким образом, бинарная математика проще для компьютера, чем что-либо ещё. Двоичная логика легко преобразуется в двоичные системы, причем True и False соответствуют состояниям Вкл и Выкл.
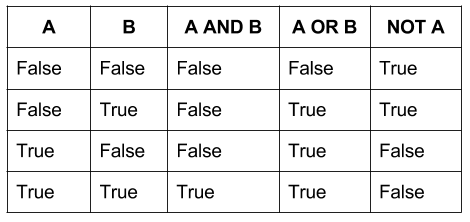
Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.